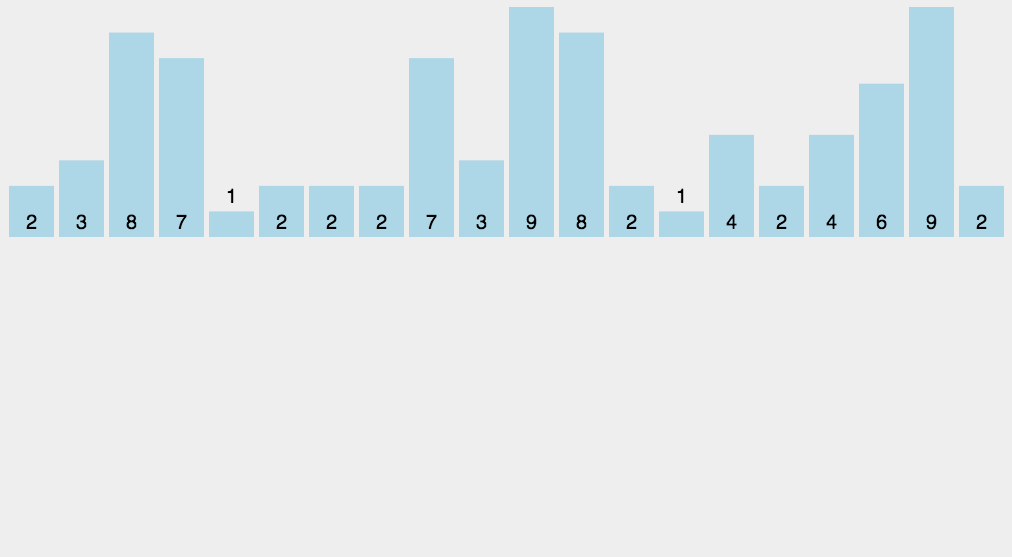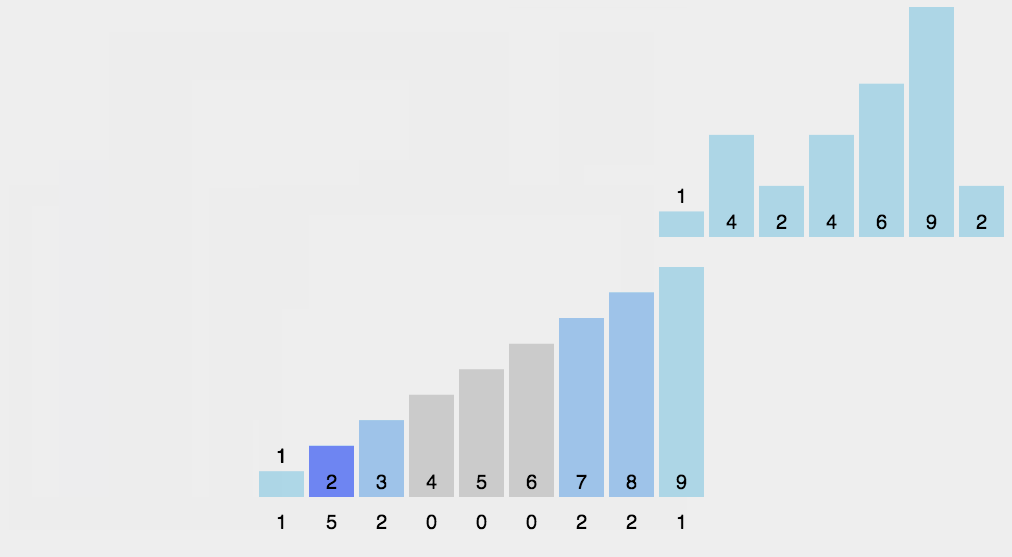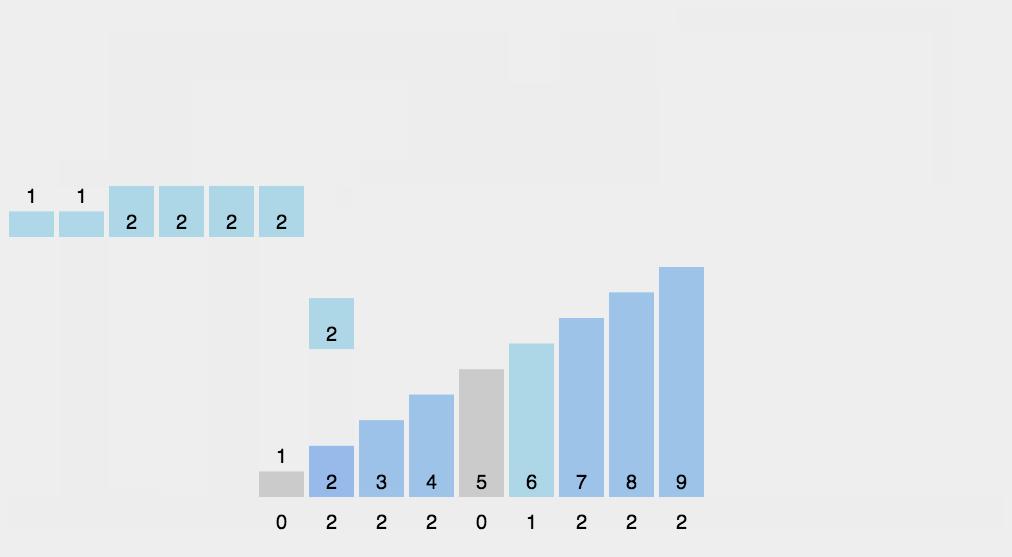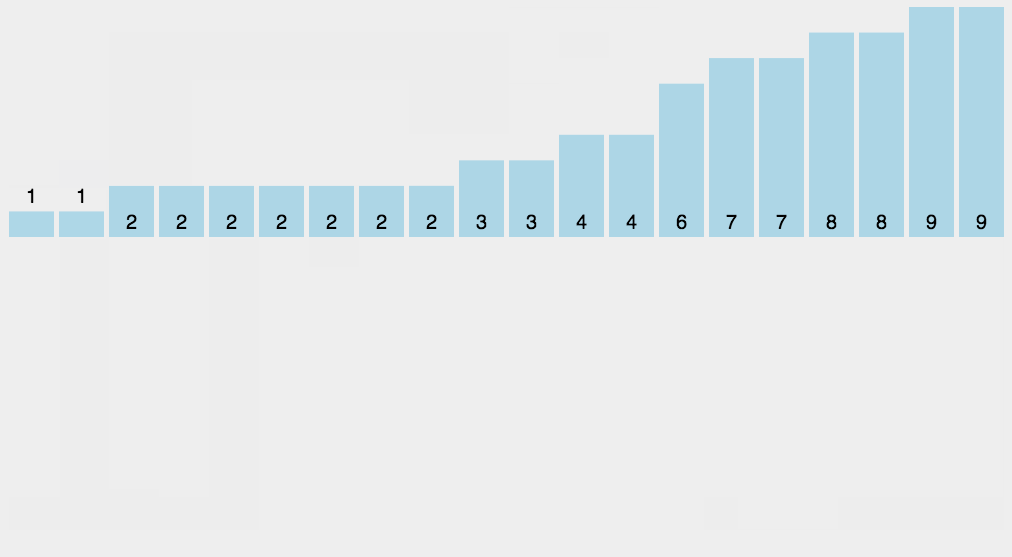STUDY/DSA
기수 정렬(Radix sort) / 계수 정렬(Counting sort)
개미606
2020. 6. 2. 17:06
1. 기수 정렬(Radix sort)
낮은 자리수 부터 비교하여 정렬해간다는 것을 기본 개념으로 하는 정렬.
문자열이나 정수 정렬에는 사용가능하며 속도도 매우 빠르지만, 부동 소숫점 실수 같이 자릿수가 없는 경우 정렬할 수 없음.
시간 복잡도는 O(d * (n + b)) == O(dn)으로 매우 빠른편.

Java 구현 코드
(1) 배열의 최대값을 찾는 함수(getMax)를 통해 배열의 최대값 찾음
static int getMax(int[] arr) {
int max = arr[0];
// 배열에서의 최대 원소 찾아 반환
for (int i = 1; i < arr.length; i++) {
if(max < arr[i]) {
max = arr[i];
}
}
return max;
}
(2) count sort를 통해 작은 자리수 부터 정렬
static void countSort(int[] arr, int n, int exp) {
int[] output = new int[n]; // 정렬된 배열을 담기위한 공간
int count[] = new int[10]; // 0부터 9까지의 자리수에 따른 정렬을 위한 배열
Arrays.fill(count, 0); // 우선 모두 0으로 채워줌
// count개수 증가
for (int i = 0; i < n; i++) {
count[(arr[i]/exp)%10]++;
}
// 누적합
for (int i = 1; i < 10; i++) {
count[i] += count[i-1];
}
// 정렬
for (int i = n-1; i >= 0; i--) {
output[count[(arr[i]/exp)%10]-1] = arr[i];
count[(arr[i]/exp)%10]--;
}
// 정렬된 배열을 복사
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}
(3) radix sort
최대값의 자리수만큼 돌기위해 재귀함수
static void radixSort(int[] arr, int n) {
int max = getMax(arr);
// 최대값의 자리수만큼 countsort
for (int exp = 1; max/exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}

+) 계수 정렬(Counting sort)
O(n)의 시간복잡도, 메모리 낭비 심함